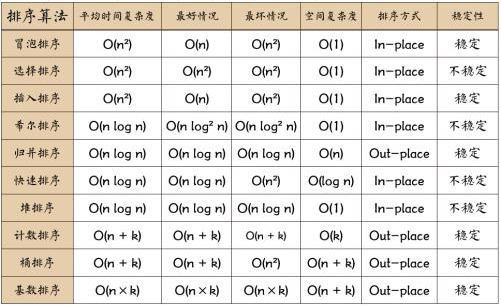
O(n)表示时间复杂度,表示的是线性阶,随着问题规模n的不断增大,上述时间复杂度不断增大,算法的执行效率越低。
按数量级递增排列,常见的时间复杂度有:
常数阶O(1),对数阶O(log2n),线性阶O(n),线性对数阶O(nlog2n),平方阶O(n^2),立方阶O(n^3),…,k次方阶O(n^k),指数阶O(2^n)。
在计算机科学中,算法的时间复杂度是一个函数,它定性描述了该算法的运行时间。这是一个关于代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述,不包括这个函数的低阶项和首项系数。
算法复杂度分为时间复杂度和空间复杂度。其作用: 时间复杂度是指执行算法所需要的计算工作量;而空间复杂度是指执行这个算法所需要的内存空间。(算法的复杂性体现在运行该算法时的计算机所需资源的多少上,计算机资源最重要的是时间和空间(即寄存器)资源,因此复杂度分为时间和空间复杂度)。
简单理解:就是变量为n的时候,算法需要对变量操作次数的量级。
比如:
要找到一个数组里面最大的一个数,你要把n个变量都扫描一遍,操作次数为n,那么算法复杂度是O(n).
用冒泡排序排一个数组,对于n个变量的数组,需要交换变量位置n²次,那么算法复杂度就是O(n²).
有时候,如果对变量操作的次数是个多项式比如n4+n2+n,取数量级最大的那个O(n4)